Calculus is a topic that is covered in Unit 2 of Mathematical Methods - you may have heard the word ‘calculus’ being thrown around from the time you were young. People tend to think it as one of the most complicated topics in maths, and despite this, it has many applications in real life. It’s a very rewarding topic!

To cover any doubts you may have about this AOS, this article will take you through some FAQs!

Q. What really is calculus?

A. There are two main types of calculus: differential calculus and integral calculus.

Differential calculus is the branch of mathematics that deals with rates of change. Integral calculus is involved with the summation of infinitely small factors to find some sort of whole (i.e. usually finding things like area, volume and length).

Q. What are some uses of calculus in real life?

A. Calculus is usually used to model systems that are undergoing some sort of change. Changes come in all sorts of forms in the world, whether it be temperature changes, population growth, energy loss, you name it! 

•       Biologists can use calculus to compute the rate of bacterial growth in a culture.
•       Calculus has lots of applications in kinematics (the study of motion). You will explore this application in your studies as well.
•       Chemical engineers use calculus when measuring the rate of flow through reactors.
•       Structural engineers use calculus when calculating the forces acting on a structure.
•       Engineers can used integrals to work out the geometry of a building.

Q. Am I expected to use first principles to differentiate functions all the time?

A. Nope! Most of the time you will use the rule for polynomial differentiation to do so. It’s much more time efficient!

However, your teacher may test your ability to use first principles in your tests or exams. In such cases, the question should state if they’d like you to use it.  Therefore, it is important that you get an understanding of how to use the formula for first principles.

Q. What is the derivative function used for?

A. The derivative function is used to evaluate the gradient at a particular point on a graph. The derivative is unique to the function, and by substituting a point on the graph into it, you will find the gradient at that particular point.

Q. What is the central difference approximation?

A. The central difference approximation gives the best approximation of the derivative function at x. It doesn’t include a limit.

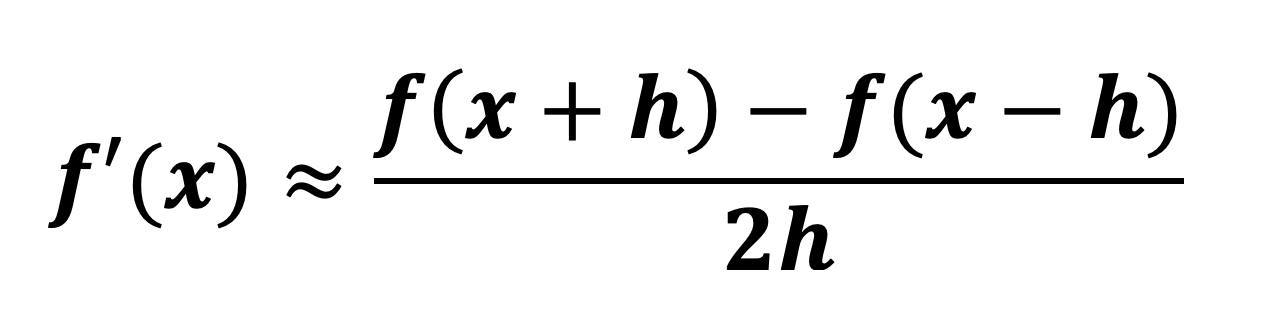
Q. What is a ‘differentiable function’?

A. A differentiable function is a function where the derivative exists at each point in its domain

• Functions are not differentiable:
• At a cusp (point section on a graph)
• When it is discontinuous
• Where there is a vertical tangent 

Q. What does the different notation used in calculus mean?

•       The derivative of a function f(x) is denoted with f’(x).
•       If you derive an equation that gives y as a function of x, you will find dy/dx. This is called Leibniz Notation and reads as ‘the change in y with respect to x.’
•       All integrals will have a ‘dx’ next to them (x can be any letter). This tells you the variable that you are anti-diffing with respect too.

Q. What sort of functions do I need to know how to differentiate/integrate?

A. In Unit 2, you are only expected to know how to differentiate and integrate polynomial functions. Next year, you will learn how to differentiate other functions such as exponentials, logarithms, and trigonometric functions.

Q. What is the difference between an instantaneous rate of change and an average rate of change?

A. The instantaneous rate of change is the change in rate at a particular instant. On a graph, this is equivalent to the gradient at a particular point.

If you wanted to find the instantaneous rate of change a point ‘a’, you need to find the derivative function and substitute ‘a’ into it.

The average rate of change is the measure of how much a function has changed over a given interval. This is measured as the gradient between the two points in question.

For example, if we wanted to find the average rate of change between point a and b on the graph of f(x), the formula would be as follows:

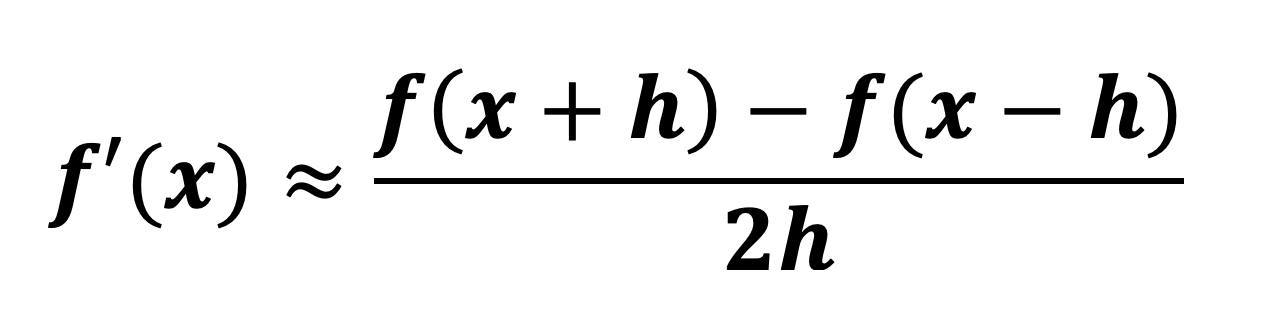
Q. I don’t understand how to prove the nature of a stationary point. How is it done?

A. To prove the nature of a stationary point, you need to find the gradient of the function on either side of the stationary point.

For example, if you had a stationary point at x=4, you could substitute x=1 (before the stationary point) and x=6 (after the stationary point) into the gradient function. When you do this, it is better to choose x vales such as 1 and 0 as it is easier to evaluate the gradient.

You then evaluate the derivative at those points – the actual value doesn’t matter, but what’s more important is whether it is positive or negative. 

•    For maximum turning points, the gradient before the SP is positive, and negative afterwards.
•    For minimum turning points, the gradient before the SP is negative, and positive afterwards.
•    For stationary points of inflection, the gradient before and after the SP is the same (can be positive or negative).

Q. Why do we need to include a +c in antidifferentiation? 

A. The +c represents any constant numbers that may have been dropped off during differentiating. Since the derivative of all constants is 0, we can never be certain if a constant was originally present or not.

Q. How can I do well in this topic?

• Here are some tips for doing well in calculus:
• Have a good understanding on how to find stationary points, the equations of tangents and equations of normals. The process to find these are very formulaic and doesn’t change much from question to question – they’ll appear in your tests and exams!
• Practise plenty of application type questions, as this is where the topic can get quite tricky. Kinematics and measurement based questions are common in calculus!
• A lot of the calculus based questions you’ll encounter can be done without a calculator (expect for some application type ones). Therefore, do lots of practise without one.
• To do well in this topic, you need to be very confident with your algebra. It is also easy to make silly mistakes so make sure you check each step as you go.
• Check your notation. Unfortunately, you will lose marks if you forget to write a ‘+C’ or a ‘dx.’

Hopefully this article clarified some of the questions you have on calculus! The best way to enhance your knowledge of this topic is to ask lots of questions: your teachers and peers are there to help you.