How to Tackle Those Tricky Projectile Motion Questions

Picture this: You're sitting in the exam or class room and come across a projectile motion question. At first glance, it seems easy enough to solve. But wait… you stare at it some more. You come to the realisation that this one looks a lot different to the conventional symmetric projectiles you practised repeatedly.

This was my story in Year 12. Every time I saw a question that sounded or looked different to the usual ones, I kept forgetting the sign conventions, equation manipulations, and rules. So, before my HSC I made a summary of the most common but different types of questions that could be tested, and how to solve them. 

In this article I'm going to take all that hard work off your plate and go through 5 commons types of unique and tricky questions you could be asked in the exam!

1. Object projected from a horizontal surface

• Initial vertical velocity u_y = 0 since there is no vertical component to the initial velocity.

• Launch angle θ = 0.

• Eg. objects dropped out of a moving object such as a plane, thrown horizontally from the edge of a cliff, fired horizontally etc.

• Use g as positive.

• Define downwards displacement as positive. For example, + ∆y = u_yt + 1/2 gt ².

• Total time of flight is equal to the time taken to reach maximum height.

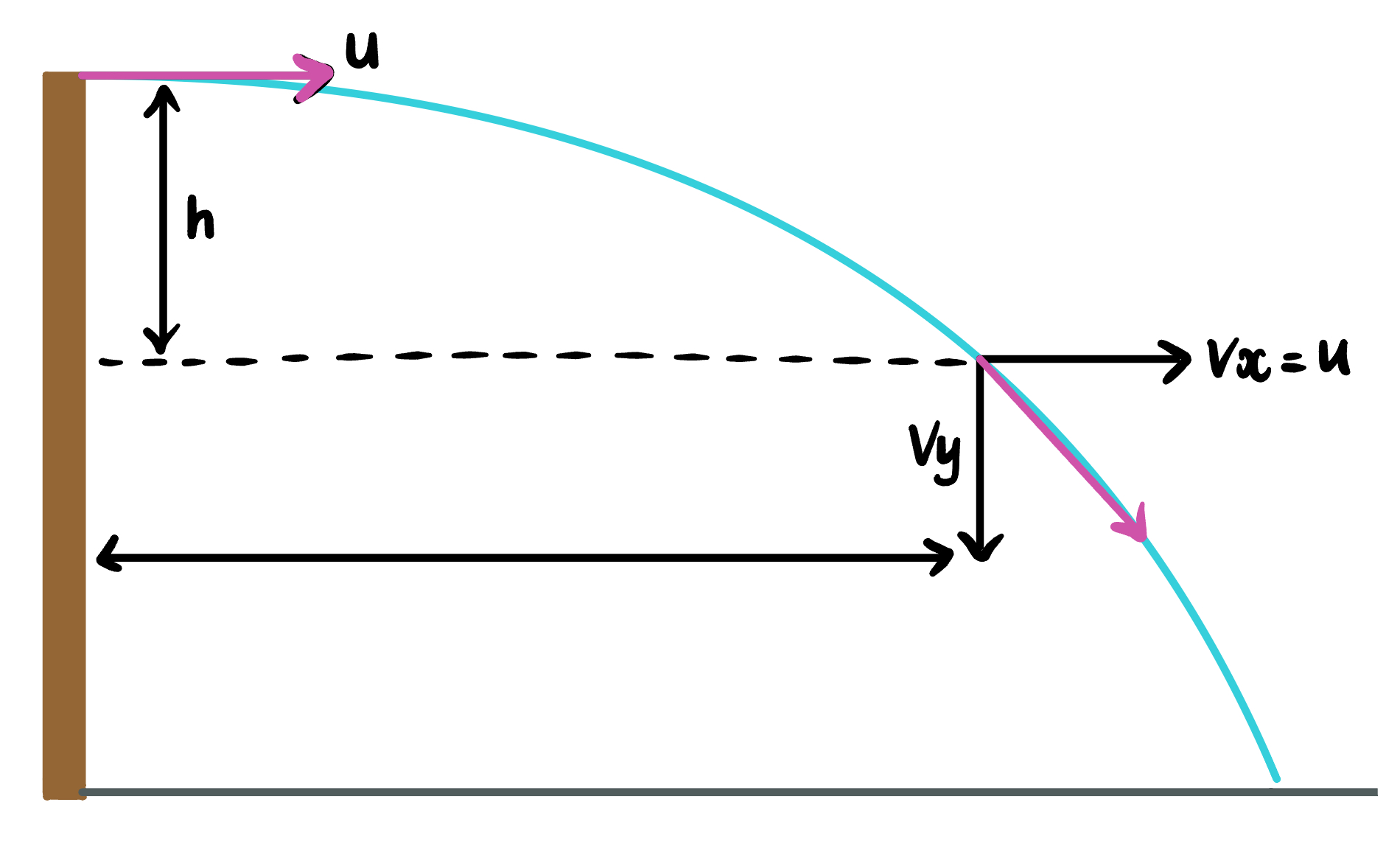
2. Object thrown up and landing at the same level

• Vertical displacement at the end of the flight is equal to zero.

• Time to rise = time to fall = half the total time of flight = time taken to reach maximum height.

• v_y at the top/halfway through the flight = 0 (maximum height is reached when this occurs).

• Speed at launch = speed at landing.

• Angle θ = angle Φ. 

3. Object landing at a different level

• Vertical displacement = difference in initial and final height.

• If target is lower than initial projection height, then vertical displacement ∆y is negative and take g as negative.

• v_y at the top is zero (maximum height achieved).

• Time is not symmetrical, i.e. time taken to rise ≠ time taken to fall.

• Final speed and angle are different to initial.

• Height above the launch position = maximum height from ground - launch height.

• The equations S_y = u_yt + 1/2 gt² and v_y² = u_y² + 2gS_y give this maximum height above launch position.

4. Object launched vertically upwards

• Initial and final horizontal velocity is zero.

5. Practical investigation 

You may be asked to perform practical investigations in class labs, for assessments or analyse related questions during exams. Below is an example of a common one and some tips to tackling a similar problem.

• Measure and use the height of the desk to calculate the time of flight.

• Measure and use range and time of flight to calculate the initial velocity. Vertical velocity is zero initially.

• You can be asked to use the conservation of energy to calculate the expected velocity of the projectile as it leaves the ramp.

At the top of the ramp:

[Use vertical height above the desk!]

GPE_i + KE_i = GPE_f + KE_f

There is no kinetic energy at the very top, before it is launched. Therefore, KE_i = 0.

There is no gravitational potential energy at the very bottom of the flight, once the path is complete and the projectile reaches the ground. Therefore, GPE_f = 0.

∴ GPE_i = KE_f

mgh = 1/2 mv_f²

∴ v_f = sqrt(2gh)

Assumptions that are made during these experiments:

• Neglecting air resistance

• Neglecting friction

• Neglecting any non-conservative forces (this is why v = sqrt(2gh) may not be accurate because in reality there are forces acting).

These conservation of energy principles can be extended to all projectiles:

• Because no other forces other than gravity are assumed to act on a body undergoing projectile motion, its total energy remains constant.

Total energy of the body = kinetic energy + gravitational potential energy = constant

• When h = 0, the body possesses only kinetic energy. As it moves upward, it slows down, loses kinetic energy and all of the kinetic energy is converted into gravitational potential energy when it reaches the maximum height. As it moves downwards, this potential energy gets converted into kinetic energy again as the projectile gains speed.