So I know that a lot of people struggle with sketching trig graphs, including me. So It has been quite a while since I last posted a math thread, just expressing the interest and passion I have for the field! So I decided to continue my trigonometry thread, by posting a guide on the basics of trigonometry graphs, and also some helpful tips on how to sketch them!
Circular functions:-
 =) A
Asin[
n(x
-c)] +
B-
 =) A
Acos[
n(x
-c)] +
B-
 =) A
Atan[
n(x
-c)] +
BThese are the three main types of circular functions, sine, cosine (me) and tangent. I have colour-coded the things that make sketching trig graphs a pain. The
amplitude simply describes how 'tall' and 'short' the graph is. It shows us the maximum value of the graph as well as the minimum value. The
horizontal translation is as usual, it describes the 'shift' that the graph takes, either a translation in the positive direction, or negative direction of the x-axis by 'c' units. The horizontal translation does not affect the amplitude what so ever, it only shifts/moves our graph sideways. The
vertical translation is as usual too, it simply tells us how many units we should move the graph, either 'B' units in the positive, or negative direction of the y-axis. The
period basically tells us how
'long' until the graph will start to repeat itself.
The amplitudeWhat is it?The amplitude basically tells us how high up the graph will actually reach, and how down low it will reach. The amplitude can be any real number, and only affects the graph in it's length, stretching it vertically! Although there may be a negative sign in front of the function, when asked to state the amplitude, we only take the positive of it. This is because, as I discussed earlier, the amplitude basically shows us the 'length' of the graph, and as we all know, negative lengths cannot exist!
Remember,
ampli-tude = how tall are you, dude?PeriodWhat is it?The period basically tells us how 'long' until the graph will become boring and lazy, and just start to repeat itself. We know that trig graphs are periodic, symmetrical, meaning that after a certain
period, they will repeat themselves. For the rest of this thread, let's assume that the period is always given in time increments, as it's the most easiest way to understand how the period works. The period for sine and cosine graphs is:

and for tangent

.
The sine function)
The sine function is probably the easiest and most simple. Now let's have a look as the basic sin(x) graph:
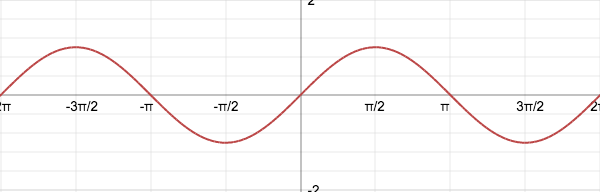
Now the best way probably to differentiate between sine and cosine graphs, is probably where they initiate. The sine graph always initiates at the origin, (0, 0). Why? Let's prove it:
=sin(x))
 = sin(0) = 0)
)
That was the most lame and vague proof haha! But Im only in year 12, not Einstein or Kinslayer, yet

As you can also see, the highest y-value is 1, and the lowest v-value is -1. This is the amplitude coming to play! f(x) = sin(x), the A=1 as we all know that invisible 1 hides behind things! Anyways, let's have a look at the alteration of the amplitude. Let's look at the graph of f(x) =2sin(x), where the amplitude is 2. So the maximum value and minimum values should be 2, -2:
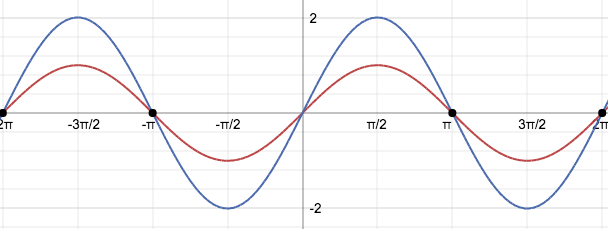
The blue graph is f(x) = 2sin(x) and the red one is the normal one. As you can clearly see, the blue one has an amplitude of 2, so it has
vertically stretched, and is now taller than the normal one! But also keep in mind that everything else has remained the same, because the amplitude only affects the the length of the graph!
Remember, ampli-tude = how tall are you, dude?Now let's look at the effect that the period plays on the graph.
The period shows us the time taken for the graph to naturally repeat itself. The first graph, f(x) = sin(x) has an invisible 'n', which is 1. So

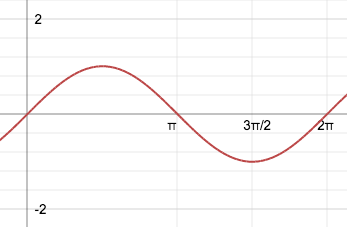
Can you see how the graph initially goes up to y=1, then down to y=-1, and then also back to where it initially started, y=0? That whole pattern, is called the period. Now I said that after every period, the graph will repeat itself, and we said before that the period is

for this graph, so if we zoom out, the graph should start to repeat right at this point, look:

Put your mouse cursor at

. Look at the shape of the graph on the left of this point. Now observe the shape to the right of this point. Oh! They're the same! Good, it means that the period is certainly

. Now the graph will continue to repeat itself at increments of

'minutes'. This pattern will literally go on forever, so we are usually asked to graph one period, because if you can get the first period correct, then the rest will just be a repeat and useless to sketch!
Now how do we know where the
x-intercepts are? And what about
where the maximums and minimums occur? Well with graphs that have no horizontal nor vertical translations, we can work out the two intercepts of the graph and the location of the maximums and minimums by dividing the period by 4. Now we divide the period by 4 because of the symmetrical patterns of the functions, and mainly because the math gods probably said so!
So if we said that the above period is

, then by dividing by 4, we get

. So, every

minutes, something HAS to happen to the graph. The pattern is max/min, intercept, max/min, intercept etc...
So let's take another look at the graph of f(x) = sin(x) and see when/where the maximums occurs, the minimums and also the intercepts.

Okay so sine graphs begin at zero, so if we add

then

, that is our first maximum, check above! So we are at

, let's add another

to find the intercept! So now we have

. This is our x-intercept! Add yet another

to our value, we now have

, and this is our minimum value! Add yet another

and we are now at

which is our next x-intercept and also our period. So let's stop here!
Okay, now it's your turn, let's do one together with the steps that I take when tackling trig graphs:
Sketch f(x) = 5sin(2x)
Step 1: What graph is it? Sine, cosine or tangent?
Spoiler
This is a sin graph, if you couldn't get this then you should've gone to specsavers!

What is the amplitude?
Spoiler
The amlitude = A = number in infront of the circular function = 5
Work out the period:
Spoiler
Period of a sine graph

Divide the period by 4, so we can see when/where the maximums, minimums and the x-intercepts occur
Spoiler
Period

. Divide the period by 4 =

. So at every

intervals, we will have something different going on with our graph.
Gather the prior information about the graph to make a conclusion for the sketch:
Spoiler
Well, we know this is a sine graph, so the basic shape is up, stop, down, stop, up, and finally stop. (Horrible attempt at me trying to describe the nature of a sine graph). Okay so if this is a sine graph, then we must start at the origin right? Also the amplitude is 5, wait what does this mean again? Oh yah,
ampli-tude = how tall are you, dude? so the highest point will be 5, and the lowest point will be -5 on the sketch. The period is

, so after every

minutes, we have to repeat the graph! Also at every

minutes, we will see something special going on.
Graph it
Some helpful links to definitely check out:
http://www.purplemath.com/modules/grphtrig.htmhttps://www.youtube.com/watch?v=RzZyyIu9IvAhttp://www.regentsprep.org/Regents/math/ALGtrig/ATT7/sinusoidal.htmhttps://www.khanacademy.org/math/trigonometry/trig-function-graphs/trig_graphs_tutorial/e/graphs_of_sine_and_cosinehttps://www.mathsisfun.com/algebra/trig-sin-cos-tan-graphs.htmlRemember, keep practicing the basics first, only then you can master the harder stuff. It is vital that we understand what is actually meant by terms like period, amplitude and such!
That ladies and gentlemen, is a really simplified and basic introduction on sine graphs. I will make another really detailed thread on how to tackle vertical and horizontal translations, but not in this thread because it is becoming too long. I hope you have even learned one thing out of this! If you have any further inquiries or if anything needs to be changed/improved, let me know.
cos(27x)

