not really a specific question. just wondering if anyone has any good ways of remembering the circular functions exact values cause i feel like a bit of a idiot waving my fingers around during a test lol 
thanks!!
Not a fan of either of the above methods. Personally, I like these triangles:
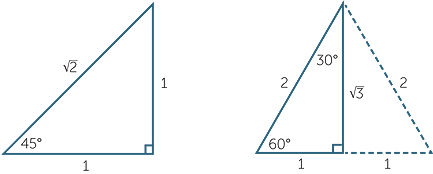
If you can memorise these, then the exact values come from the trig ratios. Eg,
sin(30)=O/H=1/2
And if you can't remember them, you can also logic them.
The triangle on the left is an isosceles triangle with two 45 degree angles, so the last one HAS to be 90. Then, just make the two same side lengths to be 1, and use pythag to find the last.
The triangle on the right is an equilateral triangle, and we've decided that all side lengths are 2. Since it's equilateral, all angles are the same - 60 degrees. If you cut it in, then the bottom side becomes length 1, the top angle becomes 30 degrees, and you can use pythag again to find the final side.
Just draw these triangles on your exam, use logic and pythag to find the side lengths, and you're good to go!

