A Topic a Day Keeps the Specialist Woes Away

[keltingmeith]

#worstpunever

So, I thought of the best way to start this thread, and at first I wanted to do it the same way as methods - take the one question that always pops up first time each year, and work with that. But, specialist likes to mix it up - so I'm going to do a bit of a two in one lesson. Today, I'm talking about mechanics and vectors, and tomorrow I'll go more hardcore into the vectors.

So, mechanics. Firstly, you need to know what a vector is. If you don't know what a vector is - at this point, you're going to need more than this little mini-series to help you out...

Now that we know what a vector is (I hope), let's talk about the bare bones of mechanics. Everybody likes to teach this in different ways, but essentially there's only three things you need to know:

1. Kinematics
2. Momentum
3. Free-body diagrams.

I'm not going to touch on the first and instead save it for later, and the second is so little I'm going to do it right here - momentum can be calculated as p=mv. If two things collide, the amount of momentum before the collision is the same as the momentum afterwards. Done, sweet, move on. So, let's discuss free-body diagrams.

Now, some people like to get really into these things. They like to discuss Newton's three laws, and derive all of the forces from that. I think that's kind of silly, but you do you. Instead, I'm just going to over each possible force they can give you:

Weight
Weight (or gravity) is the force that pulls us down to the earth's core. As far as specialist is concerned, it's always straight-down, and is always equal to mg (mass * gravity)

Normal Force
Now, if we were constantly pulled to the earth's core, we should be inside of it. The normal force is the one that magically stops this, and is always exactly the amount to stop you falling through the earth. Now, in a flat plane, this is going to be exactly equal to the weight force in magnitude (but obviously opposite in direction) - but on inclined planes, it can vary a bit. Importantly - the normal force is always perpendicular to the plane.

Friction
Friction opposes motion. As a result, you won't know the direction of the friction force unless you know the direction in which the object is trying to move. The magnitude of the friction force is always equal to mu*Normal force, where mu is the coefficient of friction. The object only moves if the force pulling it along is greater than the magnitude of the friction force.

Tension
This is the force that occurs when you pull on a rope. Calculating this is a lot more difficult, and so to do calculate it you need to know the force that the rope is moving an object.

Now, I will go through an example that uses all of these - however, here's some buzzwords. Note these down, as they will mean specific things:

Smooth = usually refers to a surface. A smooth surface will not cause friction.
Light = no weight, m=0. Usually used to refer to strings so that a tension force can be experienced, but not a weight force. Just makes things simpler.
Inextensible = exhibits a tension force when pulled - usually refers to strings, so that you know it gives a tension force.

Note these down when doing a question, as they may save you some extra calcs. So now - go to exam 1, 2013. See the attachment in this post to see what the free-body diagram looks like. Now, in this instance, I've written a friction force - this will be used later, but note that the for purposes of the 2013 exam, this force is equal to 0.

So, we want to find out what the value of T is. The first thing we need to do is resolve the weight so that it is now represented in components both perpendicular and parrallel to the plane. If you look at the picture I've draw, you'll see I've included an i and j direction. Using this, we can use trigonometry to show that:



Now - we know what m is, we know what theta is, and we know g is. So, this translates to:



Note, you can answer in terms of numbers or g - the examiners don't care. I highly recommend keeping it in terms of g.

Now, let's write the other terms out in terms of i and j - they're much easier, because all of them point in just one direction. This gives us:



Where x and y are unknown (we need to figure them out!) and mu is the coefficient of friction. Since this is a smooth surface (just for now!), mu=0. Now, if we add all of these together, we get:



So, how do we use this to find the tension? Easy - since the object isn't moving (the question told us this!), then the vector that describes the total force of the object is the zero vector. This means that:



And since y describes the tension force, T, T=5g

So, here's where it gets tricky - what if the coefficient of friction is actually 0.1? Then what is the tension force? Since the tension force is trying to pull the object up, then friction opposes that and tries to pull the object down. If there was no tension force, friction would point in the other direction. In that case, our total equation is:



So, to answer the question now, you'd have to instead start with the j component, solve for x, and then use that to find y. Not too much harder - and this is basically the accumulation of all the things they can ask about mechanics!

Note that some of you may instead prefer to write "in the x-direction:" and "in the y-direction:" - THAT IS FINE. I just did it this way to emphasise the cross-over with vectors, and get you thinking about them. Answer whatever way you are comfortable with.

---

If you're not following the methods thread, check it out here! I won't be mixing lessons, and some of it might be important to you guys in specialist! Otherwise, it's the same deal - each day, I'll put up a lesson until after both exams, so come back and stay tight each day for some hopefully-handy revision.

[keltingmeith]

And now, the follow up - vectors.

So, before we very explicitly only talked about vectors in terms of dynamics. Today, we're going to talk about them in terms of themselves, and just go over everything you can do in the vectors topics.

So, let's say you have your vector, a = xi + yj + zk, or b=ui+vj+wk. It has two properties - direction and magnitude. Direction can be determined just by drawing your vector on a graph. Another way you might choose to do this is in terms of the angle that the vector makes with each axis - more on this later. If you wanted to define the magnitude, however, you have to do this in terms of pythagoras:



Next, we can add vectors together. If you do this algebraically, it's as easy as adding is with normal numbers. But don't forget, there's also a geometric idea of adding vectors together, which looks a bit like this:



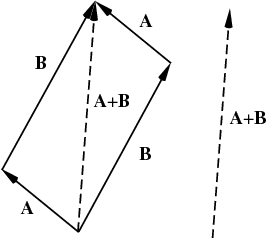
Importantly, this shows that a+b = b+a. Now, people like to assume that stuff like this is always true - it's not, and I'd show you a good example, but I don't want to be the reason for a freak-out just before an exam.

Now, we can also do multiplication and division with vectors - to an extent. If you do this with a vector and a scalar, it's very straight-forward - just pretend you're expanding brackets. And again, don't forget the geometric argument:



This also shows how you'd do subtraction geometrically - instead of thinking of your vector as a - b, think of it as a + (-b) - so you're adding a with negative b.

That's all well and good - but how about multiplying vectors together? This is much harder, and there are (believe it or not) two different ways of multiplying vectors together. In specialist, we only care about the simple form of one of these, and it's called the dot product. It can be evaluated in one of two ways:



Now, remember we talked about finding angles to axes? We can do that with this dot-product. In the case of the x-axis, we make b point in just the direction of the x-axis (so b=ui for this demonstration), and we calculate the dot product in both ways:



Where theta_x is the angle made by a with the x-axis. Now, since they're both equal to the same thing, just calculated in different ways, we can make them equal and solve for our angle:



Now, this bit might be a little confusing - but, it should be obvious that if u is positive, then it can be cancelled out from both sides with no issue. Now, if we want our angle to be with the POSITIVE x-axis, then u is positive, so that's not an issue, and we can just cancel away. This is just something to keep in mind if you copy this - if you use this formula, but you were asked to find the angle made by the NEGATIVE x-axis, your answer is actually going to be 180-the answer we get from this formula. This gives us:



And now you just need to take the inverse cosine! Feel free to this out for the other axis, you might notice a pattern forming.

Now, there's only two things left to go over - the first, is resolving into components. We've actually already done this before - in the dynamics question, instead of making the j point up and i point right, we made them point perpendicular and parallel to the plane. Us multiplying the weight by the sine and cosine of that angle? THAT'S resolving the weight vector into two different components. Now, let's say instead of knowing the angle of the plane, let's say we instead knew that it inclined along the vector b=i+j. Well, we could calculate the angle and then do what we did before, but that would get very complicated if instead the plane was a three-dimensional object. So, let's find a way to do it in terms of b, instead.

Well, we can find out that the angle made with the x-axis is 45 degrees. We also know that the dot-product has a cos in it, and in the dynamics problem, the cos and sin vectors point as shown in the attached figure (note: this is after applying the z-rule. Hopefully this helps with the last lesson, as well, if you didn't understand that part in where the angle ended up!). Using this, we know that we want our final vector to look like acos(theta) (where theta is the angle between the b-vector and the ground) to get the component that points in the j direction in our dynamics diagram. We can actually get this using dot-products:



And this gives us our desired vector length! Now, very confusingly, this is often called the parallel component - and that's because of this image:



See, while this gave us the component perpendicular to our plane, there's actually a second vector that makes the same angle to our weight vector as the plane does - but it points perpendicular to it, and what we've actually done is resolved our weight vector to this second vector. The fact is that the vector maths was developed before the inclined plane problem was, hence why the two don't make sense together - the vector definition is based on what it's always been, but there's no point defining an inclined plane based on this second vector.

However, this does make the next step make sense. Let's say that we re-define b so that it is now i - j - now, this vector is perpendicular to our original b, but points in the direction as this second vector that I mentioned before. This means that now that we have our resolved magnitude, we can multiply this by our new b-vector to get the final vector that is perpendicular to the plane. However, we don't want to include the magnitude of this b-vector, so we also need to divide by its magnitude. This gives us the final formula:



Note that the little hat indicate that we use the unit vector instead of the actual vector, calculated using the handy little equation:



Okay, so, how do we then find the perpendicular component (the one parallel to the plane - to be, you know, confusing and all that)? Well, we could do it in terms of sine, but we don't have a vector formula with a sin(theta) in it. However, we do know from the geometric definition of vector addition that:

parallel projection(a.b/|b|^2 * b) + perpendicular projection (p)=a

We can now solve this to get the perpendicular projection:



Now, I know figuring out which is parallel and which is perpendicular is going to be very confusing - read the question. Normally, VCAA are nice, because they KNOW that the wording is confusing. It's for this reason that inclined plane problems are usually approached by saying "the components parallel to the plane" and "the components perpendicular to the plane", and when doing vector resolutes, they will specifically say "find a in the direction of b" - in this case, we don't need to worry about this "second vector", we can just blindly use the equations we found earlier.

There's also only one more thing left to learn in terms of vectors! That is, independency. We say that a vector a is INDEPENDENT from two vectors b and c if you cannot construct a from scalar multiples of b and c. That is:



If you think of it like this, that means that if the vectors a, b, and c are DEPENDENT, then when you add up some scalar multiple of all three, then you return to where you started - that is, you get the zero vector. So, you can also use the equation:



where k, m, and n are not all 0 at the same time.

Proving things are independent from each other is hard. Instead, what you should do, is try to show that they're dependent - using one of the following two equations:



If you find that there is no solution to the first equation, or instead you show that the only solution to the second equation is k=m=n=0, then that shows that these vectors are independent.

[keltingmeith]

Alrighty, tomorrow, we'll start with some calculus - but TODAY, I think we're very comfortably ready (and makes sense coming off of vectors...) to talk about complex numbers.

Here's the thing - you can kind of think of complex numbers as a vector, where the real component is the i component of a vector, and the imaginary component is the j component of a vector (in other news, electrical engineers will actually use j instead of i as the imaginary number #themoreyouknow). In fact, in HSC, they actually use complex numbers as vectors (although this may have changed recently) - nobody else does, no clue why they do, but there ya go.

With that in mind, let's say we have our complex numbers - z=a+bi, and w=c+di. However, these are fundamentally different to vectors, in that doing arithmetic with them is a LOT easier. Adding and subtracting is the same as vectors:



Multiplication is just like normal numbers:



Don't forget that i^2=-1!

Division is slightly more complicated - usually, the way to go about this is to make the denominator either just real or imaginary, and then division is straight-forward. Usually, we choose to make the denominator real - which is REALLY easy to do. If you multiply a complex number by its conjugate, the result is always real. Just watch:



So, if dividing one complex number by another, multiply the top and bottom by the conjugate of the bottom, like so:



However, this can get MUCH easier. Remember how we defined vectors in terms of angles and magnitudes? This is much more common-place in complex numbers, and we call the magnitude the modulus, and the angle the argument. To make things easier, we also make the angle be the one with the positive x-axis and is in the range (-pi,pi], which means you can find it in one of two ways - either the formula we made in the vectors part, or the much easier to use one with tan:



You may also see:



Which is true, and you can do some simple algebra to show that. We'll come back to this later.

Okay, so now that we've got this, we may choose to re-define our complex numbers like so:



Where r is the modulus of the complex number, and theta the argument. cis(theta) stands for cos(theta) + i*sin(theta). In fact, if you ever want to go from this form to the first form we used (cartesian), you literally just expand the cis:



Okay, so why do we care about this new (mod-arg) form? Because multiplication and division become so much easier:



In fact, this allows us to very, VERY, easily do some exponential stuff, now:



which is De Moivre's theorem. Now, this is nice for finding powers, but SO much more useful for going the other way. But before we do that, we need to talk about why we care about complex numbers at all.

The reason comes down to something called the Fundamental Theorem of Algebra, which states that all polynomials with order n (that is, the highest power in the polynomial) has n solutions over the complex plane. What this means is if we want to apply De Moivre's theorem to solve a complex number equation, we need to keep in mind the extra solutions. For example, let's say we have:



Well, to find what z is, you just divide the argument by 3, right? Which would give:



However, what if you take -7pi/12 and multiply that by 3? You get -7pi/4, which when converted to the domain (-pi,pi] becomes pi/4. So, this second value could also be a solution. Thankfully, all the solutions are equidistant apart - which basically means that to solve:



then every solution is given by:



And you keep putting in integers for m until you've found n different solutions (make sure they're all in the right range!). These are also referred to as the roots of unity, and if you measure the angle between each solution, you should find that they're all the same.

Okay, so let's try and extend this to other systems - say, just a general polynomial:



You can actually solve this the EXACT same way you would in methods, by using the factor theorem and then doing polynomial division (or whatever method you like to factor by). These questions become easy, and basically just a challenge in reducing them to a quadratic form and then using the quadratic equation. However, there's another tool we can also use: the conjugate root theorem.

What the conjugate root theorem says is that if a polynomial has all real coefficients, then any complex roots will exist in pairs, with the second root being the conjugate of the first. In fact, try solving the above equation by hand - you should find that both i and -i are a solution of it, in accordance to the conjugate root theorem. There's also an extension to this - if all the coefficients are rational, then any irrational roots also exist in a pair with their conjugate.


The final thing you can be asked with complex numbers are about graphs - which, to be honest, is a lot and I don't have the time to go through every individual case. Personally, I recommend you go back to your textbook and just go through that - there's SO MANY different graphs they can ask you to make, and it's really just a challenge of algebra.

[keltingmeith]

Hey guys! So, I'm really sorry, but I'm absolutely flat-out dead, so I'm not going to be able to do a specialist topic today. I'm still doing methods, though, and I'll be back with spec tomorrow, so stay tuned, then!

[keltingmeith]

Alrighty - today, we're discussing calculus! Unlike in methods, where I went over how to differentiate things, I'm not doing that here. I'm also not going over how to integrate things - integration is a technique that is best taught by practice. So, if you want a refresher on basic integration, go to your textbook.

Instead, I'm going to focus on differential equations (DEs), and how to solve them. In specialist, you can only be given one of two types:



Everything else is off the table - although things can get a little tricky when we talk about kinematics, which I'll discuss by itself at the end.

So, how do you solve these types of equations? What you've gotta do is just remember that integration is the opposite of differentiation. In fact, let's work with a simple DE - f(y)=1, g(x)=x. For this, we have:



So, if we wanted to answer this question, integrating with respect to x (on both sides) gives us:



Now, remember the chain rule? You know, this one:



We can actually apply that here:



And if we do that, our DE becomes:



Which is easy to solve! Just remember your plus c - it can be on either side, but it has to be on one:



Easy! Okay, so what if we put in an actual g(y) now? Say, g(y)=1/y. Well, in this case, you just need to collect the g(y) onto the side that integrated with respect to dy - the side with the dy/dx:



Notice at the end I did a bit of clean-up - just to emphasise that the DE can be solved to give a hyperbola. Importantly, you should always leave a plus c in there - but 2*an arbitrary constant=an arbitrary constant, so don't feel like you need to dress up c in any special way. If you ever do a manipulation to it, just give it a new name and move on.

You might also be asked to find what c is - in which case, they'll simply say something along the lines "the initial conditions are x=1, y=0", in which case just sub those in:



Final answer! See, absolutely simple - not hard. They can get a bit more tricky, if VCAA try to "hide" the f(y) and g(x) distinction, like so:



So, watch out for that. But otherwise, these types of equations, solved by separation of variables, are easy, just take some practice.


It's a similar case for the second class - you just need to integrate twice. For example:



To solve this one, we integrate once:



And then integrate again:



Don't forget in the second integration you have a constant to work with, and remember to integrate that. These aren't too much trickier to find the c-values for, either, the only trick is you need two initial values - these can sometimes come in the form of "at the point (2,1), the gradient is 0), in which case you have two equations: x=2,y=1 and x=2,dy/dx=0. Or they'll say "there are two points, (2,1), and (4,3)".


Now, those are the only two DEs you'll be expected to solve, but that doesn't mean they're the only DEs you'll see. The other thing VCAA like doing is:



Now, these aren't meant to be tricky - all you need to do is LHS=RHS. So, start by finding all the values of the left hand side:



And then put them into the LHS:



and you get the RHS. Problem solved, easy! These can get into third order, as well, but it's all the same method, so don't stress about it.

---

Now, what kinematics special is that even though you can only be asked to solve one of:



they can give it to you in a form that doesn't look like those, and expect you to change the differentials, now the functions. This formula is in your formula sheet, and is super useful:



NOTE:
x=displacement
t=time
v=velocity
a=acceleration

You can show that all of these are true by simply using the chain rule (literally), feel free to go through those proofs if you want. So, let's say you have an equation of the form:



To solve that, you'd have to specifically choose the last DE:



And since both sides you divide by v, you need to include v=0 as a solution (important! Don't forget this!).

One final thing before we go - some people may have noticed I missed one form of the acceleration DE. Specifically:



I did this on purpose - this one is rubbish. It's only use is for when we have:



Let's say the integral of f(x) is F(x) - and we'll solve it two different ways:



Alternatively:



Notice how we got the exact same answer? The last form was only really useful prior to when separation of variables wasn't on the study design - now that it is, it's not really necessary. You can still use it if you want, but those are my thoughts on the matter.

[Rieko Ioane]

Hey mate, will a spesh topic a day save me from getting a shit methods study score?

Cheers.

[gnaf]

hey
how did you get your 10th line of working- the last step when only ys are left?
thanks!

[keltingmeith]

So I unfortunately, I've got an unfortunate/annoying medical condition that's just come up. It actually takes me about 3 hours to write a single post, but I can no longer sit for more than 1 hour at a time. I'm really sorry, guys, but this is going to have to be cut short.

---

hey
how did you get your 10th line of working- the last step when only ys are left?
thanks!

You're going to have to be more specific - can you quote the specific part you're talking about?

[Willba99]

awesome posts!!!